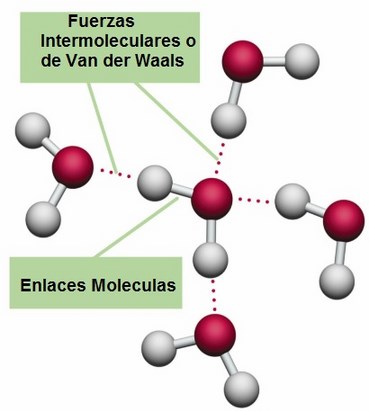
Cuando acercamos mucho dos cuerpos metálicos, idealmente dos espejos perfectos paralelos en condiciones de vacío, observamos el “efecto Casimir”; una fuerza de atracción que es directamente proporcional a las áreas enfrentadas e inversamente proporcional a la cuarta potencia de la distancia que los separa. Se hace notar en el orden de los micrómetros y es especialmente intensa en el de los nanómetros; ahí donde la teoría cuántica de campos genera sus predicciones sobre las consecuencias de las fluctuaciones de la “energía del vacío”; de ahí que fuera el mismísimo Niels Borh, en 1947, quien sugiriera hacer uso de esta teoría para intentar dar explicación a las anomalías experimentales observadas por Hendrik Casimir y Dirk Polder en los laboratorios Phillips. Hasta entonces, estos dos físicos holandeses habían estado considerando hipótesis dentro del marco de las “fuerzas de Van der Vaals” (de naturaleza electrostática), lo cual tenía sentido porque una de estas fuerzas, la más débil y la que siempre se da junto a las demás interacciones intermoleculares, es la “fuerza de London” que, entre otros efectos, es responsable de que las sustancias formadas por moléculas (o átomos) apolares puedan encontrarse en estado líquido o sólido; de no existir esta interacción, no habría atracción entre ellas y sólo se las observaría en forma de gas en todos los rangos de temperatura. De hecho, como veremos, la explicación actual del fenómeno apunta más en esta dirección que en la sugerida por Borh.

En la explicación cuántica del efecto Casimir, se postula que la naturaleza pueda violar temporalmente su principio de conservación de la energía argumentando que esto podría suceder, según el principio de Indeterminación de Heisenberg, si los eventos de creación y aniquilación de partículas y antipartículas se producen durante brevísimos periodos temporales y siempre que el promedio en esas fluctuaciones de energía sea nulo. Por otro lado, se asume que, en el vacío, éstas podrían darse en cualquier frecuencia, excepto en espacios confinados donde únicamente surgirían aquellas cuya longitud de onda cupiera un número entero de veces entre la distancia que separa las paredes del confinamiento; y, como eso supondría una limitación, sería de esperar que fuera hubiera más energía que dentro, lo que produciría una fuerza neta que tendería a reducir la distancia entre las paredes.

Sin embargo, la argumentación basada en teorías ondulatorias contradice la propia teoría cuántica, según ésta, la energía debería ser igualmente infinita dentro y fuera del espacio confinado, independientemente de la longitud de onda de las fluctuaciones que se pudieran dar en cada caso. Entonces, parece lícito peguntarse: ¿debe existir una jerarquía de aplicación de los principios físicos?, ¿es más relevante el principio de incertidumbre que el de conservación de la energía?, ¿es conveniente usar cualquier método matemático que se nos pueda ocurrir para intentar eliminar los infinitos o para justificar que unos infinitos puedan considerarse mayores o menores que otros?.. No seré yo quien dé respuesta cualificada a cuestiones pertenecientes a los dominios de la filosofía de la ciencia, pero tampoco debemos olvidar que, argumentando sobre las fluctuaciones del vacío cuántico, los físicos han obtenido la mayor discrepancia cuantitativa entre teoría y observación del valor de la llamada “constante cosmológica” que asciende a ciento veinte órdenes de magnitud, lo que debería ponernos sobre aviso en cuanto a la veracidad y/o completitud de esa teoría.

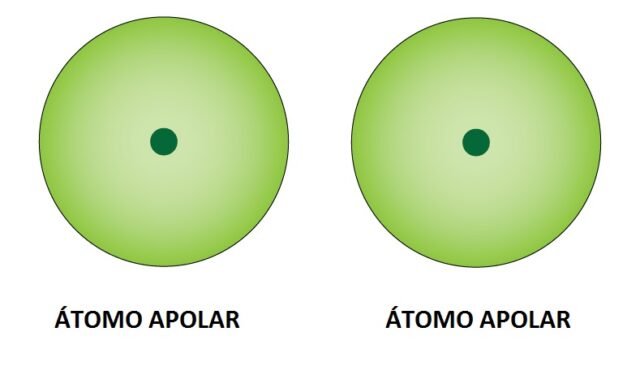
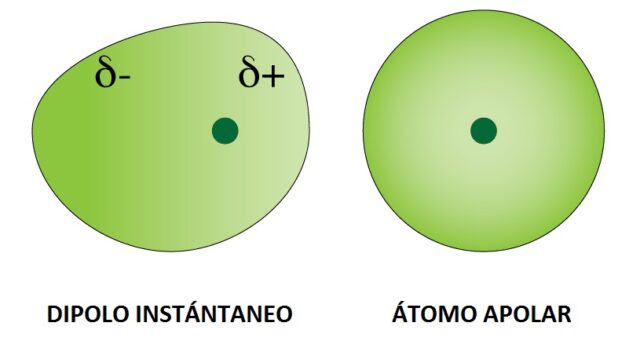
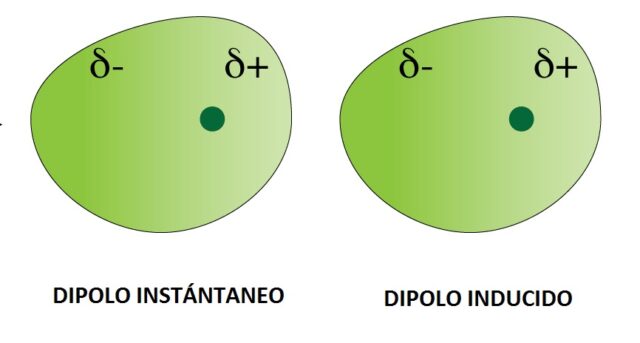
En 1955, Evgeny Lifshitz ideó una teoría de Van der Vaals generalizada que equipara la fuerza de London con la de Casimir, sustituyendo la fórmula del efecto para metales por otra que es útil en todo tipo de materiales incluidos, por supuesto, los dieléctricos. Y, es que ambas fuerzas tienen importantes nexos comunes: se manifiestan misteriosamente entre materias inconexas muy próximas (aun cuando sus cargas electrostática y magnética sean neutras), a pequeñísimas distancias sus intensidades son mucho mayores que las atribuibles a la fuerza gravitatoria generada por sus masas y, por último, las hipótesis físicas de consenso que actualmente pretenden explicar sus orígenes echan mano de cortos lapsos de tiempo inobservables, durante los cuales se producirían situaciones que darían lugar a efectos medibles y duraderos. Y es que, llevando al límite las ideas sobre las interacciones de Van der Vaals, en 1930, F. London y R. Eisenschitz, propusieron que, si bien partimos de átomos o moléculas neutras apolares, en ciertos instantes de tiempo muy cortos, éstos podrían manifestar una cierta distribución irregular de la densidad electrónica, un momento multipolar instantáneo, que induciría momentos multipolares a los átomos y/o moléculas de la vecindad y que esto se generalizaría (dispersaría) rápidamente por toda la sustancia.

Esquema de la fuerza dispersión de London

Ya en el siglo XXI, en 2005, Robert Jaffe, mostró que el efecto Casimir puede calcularse sin hacer referencia a la energía del vacío cuántico o de “punto cero del vacío”, tratándolo como una fuerza electromagnética relativista de Van der Vaals. Sin embargo, hay muchísimos físicos que, todavía hoy, siguen divulgando que el efecto Casimir prueba la existencia de un vacío burbujeante y recurren a la cuestionable propuesta de Casimir-Polder, y al principio de incertidumbre de Heisenberg, para explicar el efecto medido experimentalmente, obviando que se trata de un asunto controvertido abierto a otras hipótesis.

Siguiendo con lo que nos ocupa y dejando claro, previamente, que considero fuera de toda duda que la atracción y repulsión electrostáticas teorizadas para las fuerzas Van der Vaals tienen una importancia crucial en las interacciones entre átomos (iones) y/o moléculas que no comparten electrones (que no forman enlaces covalentes) y que todo apunta a que se pueden dar todos los supuestos de interacción de Van der Vaals descritos. No obstante, considero que las fuerzas de dispersión de London quizás no tienen todo el poder explicativo que sería deseable respecto a la descripción fundamental del fenómeno observado.

¿De qué estoy hablando?

Como todo en ciencia, la hipótesis de London-Eisenschitz, cuya aceptación es generalizada en la comunidad científica, es susceptible de ser revisada. A mi juicio, la probabilidad de que ocurra este tipo de eventos debería ser ínfima y esto la haría inconsistente con la magnitud de las observaciones. Para empezar, sería precisamente la inmensa velocidad con la que cambia la distribución electrónica de un átomo o molécula neutra y apolar la que dificultaría sobremanera que se mantuviera la supuesta fuerza de London el tiempo suficiente para generar multipolos inducidos permanentes en los átomos y/o moléculas (inicialmente apolares) contiguos; por supuesto, mucho más improbable y raro sería el que una cadena de estos acontecimientos pudiera generalizarse instantáneamente. Los átomos con menos electrones deberían ser los que tuvieran mayores posibilidades de mostrar eventos de densidad de carga especialmente inhomogénea, por ejemplo: la molécula de hidrógeno, con sólo dos electrones, presentaría una distribución muy irregular casi en todo instante; por el contrario, sabemos que son los átomos más grandes y las moléculas con mayor superficie los que con más fuerza interactúan de esta manera.

La respuesta oficial es que la polarizabilidad es un factor efectivo y esto se da, precisamente, cuando hay un mayor número de electrones implicados. Obviamente, los átomos y moléculas más grandes son más polarizables, pero la polarizabilidad se mide en el seno de campos creados al efecto o frente a iones o moléculas multipolares permanentes, que tiren de las nubes electrónicas durante el tiempo que sea necesario; sin embargo, resulta que, en la hipótesis que discutimos, estamos considerando sistemas con únicamente átomos o/y moléculas neutros de partida, sin ninguna influencia externa. En estos casos, es de esperar que la repulsión electrostática entre el gran número de electrones, el principio de exclusión de Pauli y la concentración de cargas positivas en núcleos mucho más masivos (que muestran muchas menos vibración que en el caso de los menos masivos, como el hidrógeno), procurarán que la distribución de carga eléctrica sea muy homogénea en todo momento y que sus mínimas fluctuaciones no trasciendan al resto de la sustancia más que como una suerte de pequeña vibración generalizada, fruto de la frenética actividad en estos niveles. Resumiendo: sería razonable considerar que, de producirse dipolos instantáneos, igualmente instantánea debería ser su disolución y, por tanto, éstos carecerían del tiempo necesario para generar dipolos inducidos encadenados de la forma teorizada por F. London y R. Eisenschitz.

Por otro lado, si la hipótesis de estos dos físicos fuere correcta, sería de esperar, por ejemplo, que el punto de fusión de una sustancia formada por moléculas apolares variara significativamente en presencia de un campo electromagnético artificial próximo que ayudara a precipitar la creación de dipolos instantáneos en su seno y, que yo sepa, esto no se observa en la práctica.

Y… ¿qué otra explicación podría ocurrírsenos?

En el marco del nuevo paradigma que ofrece la Teoría de Ruedas, puedo avanzar una hipótesis que es consistente con las observaciones del efecto Casimir y la fuerza de London que surge de la descripción previa del modelo que explica las peculiares propiedades de las partículas subatómicas y que presenta una imagen concreta del átomo radicalmente alejada del modelo difuso y probabilístico de la teoría cuántica.

En mi modelo de átomo los electrones están rebotando continuamente sobre los protones del núcleo gracias a la combinación de efectos: las fuerzas electrostáticas (que atraen a ambos), al efecto de impulsión de las ruedas (que amortigua el choque entre los dos e impulsa lejos al electrón) y al efecto de absorción de las ruedas (que ayuda a los electrones en su intento de escapar de la influencia electrostática de los protones y también mantiene a los nucleones fuertemente unidos en un pequeño volumen central).

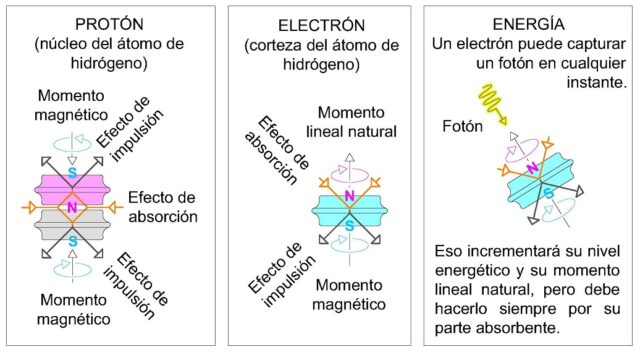
Las fuerzas electrostáticas son de sobra conocidas por los científicos, pero los otros dos efectos son completamente ignorados. Es, concretamente, el último (el efecto de absorción) el que desempeña el papel protagonista en esta nueva descripción del efecto Casimir y las fuerzas de dispersión de London, porque los electrones que están rebotando tienen su parte absorbente orientada hacia el exterior en todo momento -excepto cuando se produce la unión de un electrón con un protón del núcleo (con la denominada “fuerza débil”) para formar un neutrón, pero eso no viene al caso ahora-. Como digo, los electrones de la corteza atómica luchan continuamente contra de la atracción electrostática de los protones del núcleo valiéndose del efecto de absorción, dando mayor impulso al electrón cuando este absorbe algún fotón que lo aleja aún más y lo lleva a un nuevo nivel energético -o a escapar del átomo (es el caso del efecto fotoeléctrico, si el fotón absorbido tiene la energía mínima requerida), lo que, por cierto, tampoco viene al caso-. A lo que vamos: tanto en los alejamientos, como en los acercamientos, así como, en el instante en que el momento lineal del electrón es nulo porque éste cambia de sentido y se mantiene inmóvil en el punto de máximo alejamiento del núcleo, los efectos de absorción de todos los electrones del átomo, sumados y repartidos en todas las direcciones hacia o desde donde éstos rebotan, apuntan hacia el exterior y se hacen notar en el entorno próximo a muy cortas distancias.

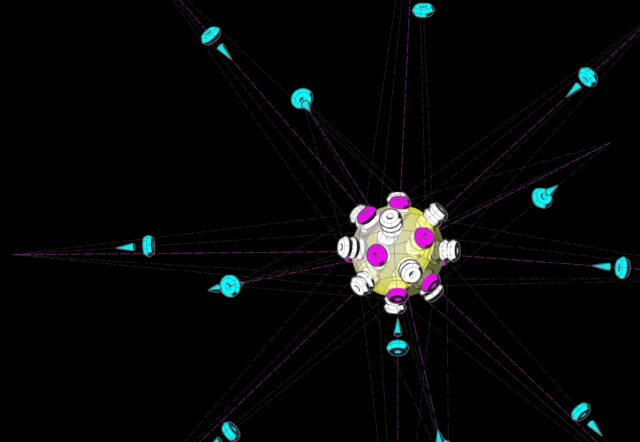
En la figura siguiente, represento el efecto de absorción de los electrones como un cono espiral de color amarillo. A la izquierda, un electrón que se aleja del núcleo; en el centro, un electrón en el punto de máximo alejamiento de su nivel energético; arriba a la derecha, un núcleo atómico de magnesio; y, debajo de éste, un electrón acercándose al protón contra el que rebotará.  

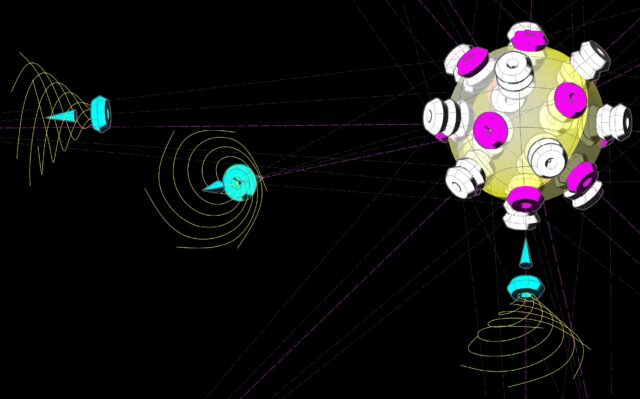
Una pésima analogía para un átomo sería la de un juguete como el de la imagen siguiente, una bola de ventosas. Es horrible porque la atracción entre electrones de diferentes átomos es un efecto a distancia, como el electromagnetismo o la gravedad, no como las ventosas que (en nuestro nivel macro) necesitan del contacto y se valen de la humedad y la presión ambiental para funcionar. Pero, aún siendo una mala analogía, la podemos completar imaginando que cada ventosa fuese una pequeña aspiradora, orientada hacia el exterior en todo instante, que trabaja para que los átomos de la vecindad se aglutinen, incluso siendo apolares y sin tener que compartir sus electrones. La distancia final entre átomos o moléculas es establecida por la bien conocida fuerza de repulsión electrostática entre cargas de igual signo.

Tan mala como la anterior sería la analogía de los tentáculos de un pulpo para visualizar el efecto en una molécula compleja.

Sin embargo, un magnífico ejemplo de cómo la evolución natural de las especies es capaz de aprovechar todas las soluciones posibles que ofrece la naturaleza, ante un reto dado, es la fantástica adherencia de los pies de algunos geckos, por ejemplo: las salamanquesas, que se han adaptado para «pegarse» a casi cualquier superficie con una fuerza increíble. Se han hecho varios experimentos para intentar entender el origen de esta cualidad y hace tiempo que se descartaron cosas como: la tensión superficial de algún líquido, la absorción por micro ventosas o los micro garfios (como los de Spiderman).

Pareciera que la adherencia pudiera ser una cualidad intrínseca del material con que están hechos los numerosísimos y finísimos pelitos (setae) que forman las almohadillas de sus dedos y que, a su vez, están divididos en microscópicas ramificaciones, terminadas en forma aplanada, llamadas spatulae; pero, resulta, que éstas no están compuestas de ninguna sustancia exótica, sino de queratina endurecida e hidrófoba como la que forma nuestro pelo, piel o uñas.

Lo realmente importante aquí es la maximización de superficie de contacto. Da igual que el animalito esté vivo o muerto, la adhesión es pasiva (no requiere de actividad vital alguna) y las investigaciones han concluido que debe tratarse de una interacción intermolecular electrostática tipo Van der Vaals; y, aunque no he encontrado ninguna alusión directa a la fuerza de London, debo entender que se refieren a ella, ya que se ha medido el mismo nivel de adherencia de las almohadillas de los geckos en el dioxido de silicio (siendo una molécula polar) y el arseniuro de galio (apolar). Si no fuera así, si los dipolos estuvieran fijos en las spatulae para inducir la polarización de las moléculas apolares de las superficies con las que entra en contacto, la adherencia sería diferente cuando se situaran sobre un material polar o apolar y esto no es lo que se ha observado.

Por tanto, si recurriéramos únicamente a la fuerza de London para explicarlo, asumiendo que los dedos de los geckos no están previamente polarizados, habría que explicar también cómo es posible que se produzcan los trillones (por decir un número muy grande) de dipolos instantáneos, seguidos de otros tantos inducidos, en el tiempo que un gecko corre veloz por una superficie lisa para capturar una presa o para escapar de un enemigo. También habría que explicar cómo es que un sólo pie de gecko puede adherirse con una fuerza de 10N. Yo no lo concibo y estoy convencido de que la respuesta está, una vez más, en la fuerza de absorción de los electrones de la corteza atómica.

Independientemente de que las moléculas puedan ser apolares o multipolares, o de que sus momentos polares sean permanentes o inducidos, siempre se producirá este efecto y únicamente estará condicionado por el número de electrones implicados, por la cantidad de superficie de la corteza electrónica de las moléculas expuesta al exterior en los diferentes estados energéticos y por la distribución electrónica de cada supuesto. Una consecuencia inmediata de esto es la diferente viscosidad de cada sustancia a una determinada temperatura, esto es: cuando la temperatura es baja la distribución electrónica es más compacta y los electrones tienden a rebotar en los núcleos de forma más homogénea. En estas circunstancias las moléculas con más superficie expuesta, incluso las apolares, son más “pegajosas” y pueden formar sólidos, es el caso de la cera de parafina de las velas. Conforme aumentemos la temperatura, los niveles energéticos más alejados serán ocupados por algunos electrones cuya fuerza electrostática individual es muy superior a la de su efecto de absorción y que, además, apantallará el efecto de absorción de los electrones que quedaran por debajo, más cerca del núcleo; por eso, la viscosidad baja al aumentar la temperatura, porque el efecto se minimiza, aumenta la distancia intermolecular y el sistema tiende a estados más fluidos y desordenados.

Por supuesto, soy consciente de que se trata únicamente de un modelo gráfico, basado en las observaciones experimentales que se han venido sucediendo hasta la fecha, pero, confío en que, una vez sea expresado convenientemente en una fórmula matemática completa para el efecto Casimir y la fuerza de London, servirá para cuantificar con mayor precisión la intensidad de esta fuerza y para predecir las temperaturas de cambio de fase de las distintas sustancias (incluso antes de que se creen en los laboratorios), así como, la viscosidad y otras propiedades físico-químicas que pudieran ser explicadas total o parcialmente mediante el conocimiento profundo de la especial dinámica de las ruedas. Por cierto, todos los resultados experimentales relacionados con el asunto que nos ocupa deberían ser considerados como indicios y pruebas de la existencia del efecto se absorción de las ruedas.

Y, ya que estamos lanzados y nos hemos venido arriba, ¿por qué no os cuento qué pruebas o indicios empíricos existen de que las ruedas generan también el efecto contrario, el de impulsión?

Vale, no hay que abusar… quizá sea mejor que lo dejemos para una nueva entrada en el blog.