Terminé la primera parte de este monográfico sobre los quarks proponiendo el siguiente postulando: los «mesones primordiales» son los únicos constituyentes fundamentales de toda la «materia». De ser correcto, todas las partículas masivas estarían constituidas por un número entero de estos mesones y, si somos capaces de deducir el valor de su masa, sólo tendríamos que multiplicar ambos números para inferir la masa en reposo de cualquier otra partícula, incluidos leptones, nucleones y, por supuesto, los quarks de la segunda y tercera generación.
A primera vista parece sencillo, pero no lo es en absoluto. En primer lugar, en el mundo subatómico lo frenético es lo habitual y el problema del cálculo de la masa en reposo de la materia que se mueva a velocidades relativistas no está, ni mucho menos, resuelto. Einstein supo entender extraordinariamente bien la naturaleza interdependiente del espacio y del tiempo, pero la teoría de la Relatividad Especial no resuelve satisfactoriamente las cuestiones relacionadas con la masa y la energía porque estos dos términos se muestran como «no invariantes» con el cambio de marco de referencia, como sería de esperar de una teoría que estudia precisamente las cuestiones relativistas. Está claro que, ante la falta de ideas para solucionar este problema, se optó por tirar para adelante y aprovechar la parte de la teoría que sí funcionaba correctamente. En palabras del propio Einstein:

«No es bueno introducir el concepto de masa de un cuerpo en movimiento, para el cual no se puede dar una definición clara. Es mejor no introducir un concepto de masa distinto que la «masa en reposo» m.»
Por si fuera poco, también nos encontramos con la extrema dificultad técnica para medir la masa de los quarks más livianos, los de la primera y segunda generación del modelo estándar. Hoy por hoy, sólo se puede hacer una estimación recurriendo a la teoría vigente que, a poco que le exijas, te pide resolver infinitos términos en las ecuaciones. Así que, cuando consultemos estos valores en la Wikipedia, no olvidemos que son únicamente aproximaciones basadas en el paradigma actual.
| Modelo estándar | Sabor | Masa (en MeV/c² ) | Valor medio (en MeV/c² ) |
| Primera generación | Up (arriba) | 1,7 – 3,1 | 2,4 |
| Primera generación | Down (abajo) | 4 – 8 | 6 |
| Segunda generación | Strange (extraño) | 80 – 130 | 105 |
| Segunda generación | Charm (encanto) | 1.150 – 1.350 | 1.250 |
| Tercera generación | Bottom (fondo) | 4.100 – 4.400 | 4.250 |
| Tercera generación | Top (cima) | 169.100 – 172.700 | 170.900 |
Ya hemos visto que los quarks de la primera generación podrían no ser partículas, sino la forma que tenemos de referirnos a los extremos indivisibles del mesón primordial, pero no debemos descartar que las suma de la masa de ambos, calculadas con la teoría actual, pudiera sernos de ayuda para estimar el posible valor de la masa de los mesones primordiales porque, aunque sustituyésemos el actual paradigma por otro, no desecharíamos todo lo aprendido con las teorías anteriores. Aprovecharíamos aquello que pueda resultarnos más práctico, como hicimos, por ejemplo, con la mecánica newtoniana que seguiremos usando siempre que, para resolver una cuestión determinada, no tengamos que introducir parámetros relativistas.
Así es que, para una estimación preliminar de la masa del mesón primordial, sumemos el valor medio de la masa del Up y el Down, esto es: 8,4 MeV/c². Ciertamente, con un margen de error muy grande, pero algo es algo…
Sigamos observando la tabla de masas de los quarks, vayamos ahora a los de la segunda generación. ¿Ves algo extraño, aparte del nombre de uno de los quarks? Ahí hay algo que ha llamado poderosamente mi atención y que me pasó desapercibido cuando estaba preparando mi teoría. Podría existir una relación directa entre la media de sus masas: Un quarks Charm tendría una masa equivalente a la de 12 quarks stranges.
Pero la cosa no se queda ahí. Ahora divide la masa media del Strange entre la que hemos estimado para el mesón primordial. El resultado es 12,5. Hemos postulado que este tipo de mesones es indivisible, por tanto, debemos buscar un número entero y, como la naturaleza tiene la sana costumbre de ahorrase esfuerzos, lo más lógico es que debamos decantarnos por el menor, esto es, el 12. Otra vez 12.
Qué curioso, ¿verdad? Qué cosas surgen de un razonamiento tan «simple». Se podría decir que es una tontería, una estupidez o una simple coincidencia. Sin embargo, esa «coincidencia» también me ha llevado a valorar la posibilidad de que me quedara corto en la estimación del número de mesones primordiales que serían necesarios para iniciar la primera fase de la evolución de la materia hasta la formación de «el copo», la primera estructura bidimensional surgida de la interacción sencilla entre mesones primordiales o, como dije en el libro: compuesta de parejas de quarks de la primera generación. Recuerda que el número de quarks debía ser múltiplo de 2, por estar incluidos en los mesones, y también múltiplo de 3, para formar los triángulos estructurales de las ruedas.
En su momento, descarté el copo de 6 mesones porque las estructuras serían más complejas en las siguientes fases y me pareció que la complejidad posterior del de 9 mesones era asumible. Ahora me doy cuenta de que, de haber optado por el copo de 12 mesones al principio, todo hubiera sido más sencillo después, ya que las relaciones triangulares entre gluones se habrían establecido incluso con mayor naturalidad y las ruedas estarían constituidas únicamente por «palas sencillas» y no por dobles, donde cada una de estas palas sería uno de estos «nuevos copos» de 12 mesones primordiales.
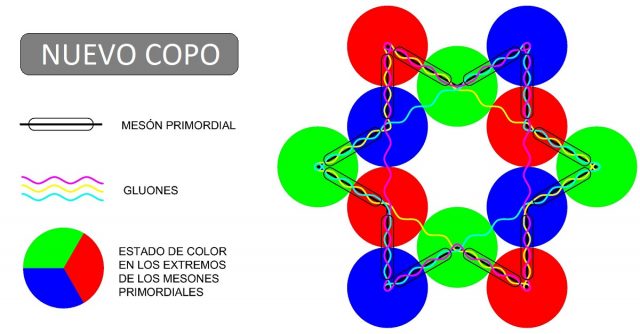
Te preguntarás: ¿qué tiene que ver esto con los quarks de la segunda generación?
Pues, verás…, resulta que, de ser cierta esta nueva hipótesis, el «nuevo copo» de 12 mesones, que formaría cada una de las «palas sencillas» de la rueda, no sería otra cosa que el quark Strange pues, dada la simplicidad y la robustez de su estructura bidimensional, se mantendría extrañamente estable mucho más tiempo de lo que los científicos podían llegar a explicar en su momento. De ahí su nombre: «extraño». Además, con esto, seguimos acotando la masa del mesón primordial: dividiendo el valor medio de la masa del quark Strange (105 MeV/c²) entre doce, llegamos a 8,75 MeV/c².
Y, puestos a especular, por qué no incluir en esta discusión a la teoría de cuerdas; por qué no contemplar la posibilidad, que ya mencioné en la primera parte, de que los mesones primordiales pudieran describirse como algo parecido a las cuerdas abiertas más simples; y por qué no añadir una nueva suposición: los quarks stranges son la versión más sencilla de cuerda cerrada, constituida por 12 cuerdas simples unidas entre sí, formando un anillo bidimensional en el cual se confinarían o compactarían el resto de dimensiones que la teoría requiriese.

Bueno, y… ¿qué ocurre con el quark Charm?
Por lo visto, no podemos descartar que esté compuesto por 12 stranges que, a su vez, estarían formados por 12 mesones primordiales. En total 144 mesones fundamentales.
En cuanto a su forma… habría que tirar de nuevo de imaginación y suponer que la estructura de estrella de seis puntas de los «copos» (los stranges) le permitiría adoptar formas variadas. Igual que ocurre con las superficies formadas por los enlaces hexagonales entre los átomos de carbono que pueden ser: planas, tubulares, esféricas, etc. Pero no me atrevo a concretar mucho más porque, según mi teoría, estas estructuras no tendrían ninguna función en la posterior formación de los átomos.
Por otro lado, también podríamos suponer que exista alguna relación entre las masas de los quarks de la tercera generación, o entre los de la tercera y la segunda, por ejemplo: la masa del Bottom es unas 40 veces la del Strange, el equivalente a 8 ruedas, y la del Top unas 40 veces la del Bottom.

¿Y… eso nos sirve para algo? Ese doble 40 no nos dice nada en cuanto a la forma espacial de las estructuras de los quarks de la tercera generación, pero ten en cuenta que los valores de las masas de estos quarks más pesados son más precisos, por tanto, pueden resultar útiles para afinar algo más el posible valor de la masa de los mesones primordiales.
Además de todo lo anterior, el modelo de la teoría de ruedas ofrece otra vía para acercarnos al valor de la masa de estos mesones primordiales, esto es: partiendo del valor conocido de la masa del protón.
La masa del protón es aproximadamente 938,272 MeV/c², pero siempre entendiendo que se trata de dos ruedas girando a velocidades relativistas sobre un eje común. Así es que, para calcular su masa máxima en reposo, debemos suponer que en los extremos de la estructura no se superará la velocidad de la luz (c). Por tanto, la velocidad media de giro de los copos de la rueda, medida en el centro de masas de cada uno, será como máximo 1/2 c.

Según mi teoría, la contracción relativista de las longitudes es equivalente (proporcional) a la contracción relativista de la masa y, haciendo el cálculo, la masa en reposo de un protón no debe ser superior a 1.083,423 MeV/c².
Cada una de las dos ruedas tiene un número determinado de «palas simples» (nuevos copos, los quarks stranges). Si consideramos que el número de palas de la rueda fuese igual a cinco, un quark strange no debería superar los 108,342 MeV/c². Este valor se encuentra cerca del valor medio estimado y, si probamos a hacer la extrapolación de este dato con todos los supuestos anteriores, dando prioridad a las masas de los quarks más pesados, nos quedaría algo así:
| Teoría de ruedas | Sabor actual | Relación entre masas | Valor estimado (en MeV/c² ) |
| Mesón primordial | Up (arriba) Down (abajo) | Up + Down | 8,81 – 9,00 |
| Nuevo copo | Strange (extraño) | 12 (Up + Down) | 105,69 – 107,94 |
| Otras combinaciones | Charm (encanto) | 12 stranges | 1.268,28 – 1.295,28 |
| Otras combinaciones | Bottom (fondo) | 40 stranges (8 ruedas) | 4.227,5 – 4.317,5 |
| Otras combinaciones | Top (cima) | 40 bottoms | 169.100 – 172.700 |
Y eso es importante porque se supone que es en esa horquilla de masas, 8,81 – 9,00 MeV/c², donde deberíamos centrar los esfuerzos para la detección directa de la materia oscura que, según mi teoría, la podríamos encontrar básicamente: formando amasijos amorfos y desestructurados de estos mesones primordiales o en forma de larguísimas y estrechísimas hebras, unidas gracias a las cargas polarizadas de sus extremos a los que hemos tenido a bien denominar Up y Down.


Pero no lancemos las campanas al vuelo tan alegremente. También podría ser que la rueda estuviera formada por seis palas. En ese caso, un quark strange no debería superar los 90,28 MeV/c², un valor alejado de la media, aunque dentro del rango estimado. Esto implicaría, por supuesto, que la masa del mesón primordial no debería ser mayor que 7,52 MeV/c² y que las relaciones entre las masas de los quarks más pesados tendrían que ser distintas a aquellas con las que he estado especulando.
Eso, claro está, siempre que sea correcta la suposición de que los bordes de la estructura del protón no pueden superar la velocidad de la luz al girar y siempre que los cálculos actuales de la masa de los quarks no sean completamente incorrectos.
Al final, será la experimentación la que acote el valor de la masa de las partículas de la materia oscura, la de los mesones primordiales, y será ese valor el que nos diga si la rueda tiene cinco o seis palas, es decir, nos dirá si la rueda es un pentaquark, con cinco quarks stranges, o un hexaquark con seis de estos «nuevos copos».
En definitiva, no dejemos nunca de cuestionar aquello que no parezca encajar de forma natural y de intentar encontrar respuestas coherentes. No dejemos nunca de darle vueltas a las teorías y, cuando creamos haber hallado esas respuestas, pongámoslas a prueba, mostrándonos siempre dispuestos a rectificar. Fomentemos la experimentación que se pueda desarrollar para probarlas, o para falsarlas, sin poner el foco únicamente en el paradigma vigente, porque, aunque cosechemos innumerables resultados nulos, será la experimentación la que nos dé o nos quite la razón.