El positrón
Cuando se hacen colisionar protones en los aceleradores de partículas, es común que aparezcan lo que, en principio, se identifica como positrones (radiación β+), los supuestos antielectrones. Sin embargo, su momento angular es el de la materia común. Por tanto, según esta teoría, no es autentica antimateria. Me explico:
Los protones están formados por dos ruedas, una con carga eléctrica positiva y otra neutra, en determinadas circunstancias esta unión puede romperse; bien por la destrucción de una ellas, bien debido a otras interacciones de las que hablaremos más adelante. En cualquier caso, podremos detectar más fácilmente la liberación de la rueda que está cargada positivamente. Una rueda idéntica al electrón, aunque con carga opuesta, es decir, un positrón libre. Si se produce un encuentro de los dos, a su velocidad normal, se comportan casi igual que si se aproximasen un electrón de materia común y su homólogo de antimateria, se desintegran. Pero no ocurre lo mismo si se les pone cerca después de decelerarlos. La aspiración de uno se puede alinear con la impulsión del otro y se puede formar un dúo, que podría confundirse con un muón neutrino (pues, al igual que éste, sería neutro) o incluso pueden simular, durante un corto espacio de tiempo, ser un átomo exótico (el positrónio); se trata de dos ruedas con carga opuesta, que rebotan del mismo modo que en el átomo de hidrógeno, pero en cuanto se colocan con las aspiraciones enfrentadas, se aniquilan. Si el positrón fuera auténtica antimateria se destruirían en el primer acercamiento; pues, en ese caso, su momento angular y su carga eléctrica serían contrapuestos. Si queremos fabricar un seudo-antiprotón solo tenemos que crear las condiciones necesarias para que un electrón y una rueda neutra se encuentren con sus lados absorbentes enfrentados, a velocidades discretas, la fuerza de aspiración hará el resto, se unirán igual que un protón pero tendrá carga negativa. Acercando un protón y un seudo-antiprotón podemos crear otro átomo exótico de corta vida, el potronio, simularán ser un átomo hasta que se atraigan mutuamente por la parte de las ranuras absorbentes y se aniquilen. Con un positrón y un seudo-antiprotón podemos fabricar un seudo-antihidrógeno, e incluso un seudo-antineutrón. Todos son entes de laboratorio, pero no son antimateria, por mucho que se le parezcan. Y, para evitar tener que poner el prefijo seudo-, a partir de ahora, utilizaré el nombre de positrón asumiendo que es parte del protón, por tanto, materia común y al homólogo de antimateria del electrón, con momento angular y carga eléctrica contrarios, lo llamaré «antielectrón».
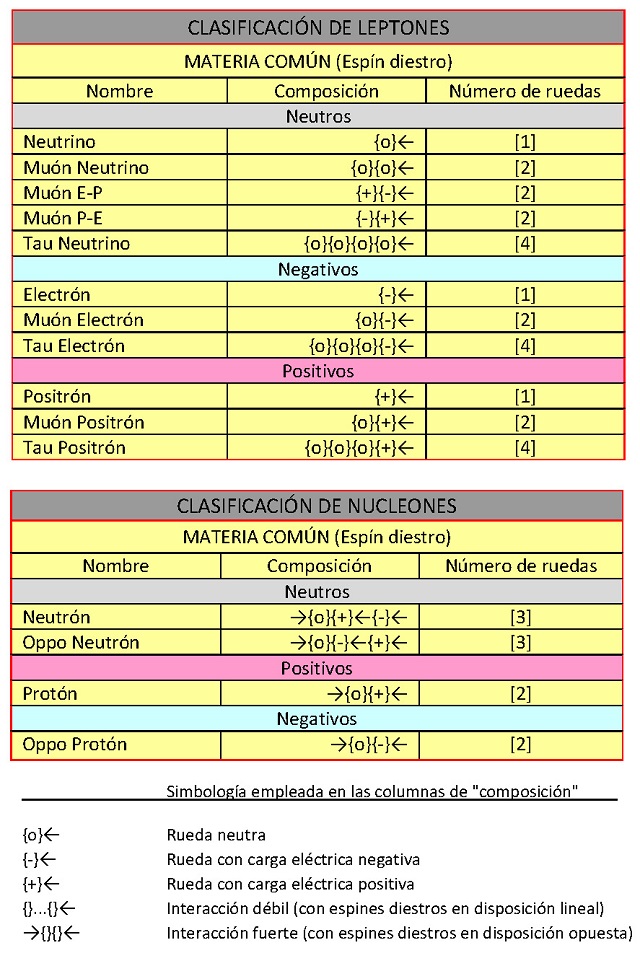
Clasificación de las ruedas y antirruedas, según sus agrupaciones
Esta teoría describe las interacciones de las ruedas, de donde se deducen los tipos de agrupaciones que se pueden dar, lo que genera la necesidad de clasificarlas en función de nuevos criterios. El primer criterio es separar claramente, en tablas distintas, la materia común de la antimateria, que se distinguen por su momento angular o espín. Cada tabla estará distribuida simétricamente con los entes de materia común a la derecha y los de antimateria a la izquierda; así será fácil centrarse en la materia común, dado que aún no hemos encontrado ningún caso real de antimateria en la naturaleza. Como segundo criterio dividiré las agrupaciones en dos tablas más: una de nucleones, aquellas agrupaciones susceptibles de formar parte del núcleo atómico, y otra de leptones, nombre que mantengo, por su apariencia relativa ínfima, para las entidades individuales y las agrupaciones lineales de éstas exclusivamente.
Nótese que he aprovechado esta nueva clasificación para reponer al neutrino y al antineutrino sus nombres naturales, según sea su espín. Así mismo, he asignado a los homólogos antimateriales del electrón y el positrón los nom-bres naturales de antielectrón y antipositrón respectivamente. Por otro lado, he incorporado dos nuevos leptones neutros, uno de materia común y su homólogo de antimateria, el «Muón E-P» y el «Muón Anti E-P» formados por dos ruedas y dos antirruedas respectivamente (electrón-positrón y antielectrón-antipositrón); que podrían confundirse con un Muón Neutrino y un Muón Antineutrino respectivamente. Como veremos, estas dos formaciones leptónicas son los que explicarían la «creación de pares», partiendo de fotones de alta energía. En la clasificación incluyo, como variedades de laboratorio (no naturales): al «Muón P-E» y al «Muón Anti P-E» (positrón-electrón y antipositrón-antielectrón, respectivamente); así como: al seudo-antineutrón y al seudo-antiprotón; a los que renombro: «Oppo Neutrón» y «Oppo Protón», respectivamente (del latín oppositus, por el orden opuesto de sus cargas eléctricas); a sus homólogos de antimateria: «Oppo Antineutrón» y «Oppo Antiprotón». Por último, he de aclarar que el orden de la composición de los muones y taus: electrónicos, positrónicos y sus homólogos antimateriales; puede ser variado, ya que no hay razón para pensar que las ruedas con carga tengan, necesariamente, que ocupar la cola en el «tren de interacciones lineales» (las uniones, por interacción débil, de varias ruedas consecutivas).
Todos los leptones y nucleones pueden descomponerse en un número determinado de ruedas con cargas eléctricas: neutras, positivas o negativas; es decir, en: neutrinos, positrones o electrones. En esta descomposición siempre se conserva el número de ruedas [entre corchetes] y la carga eléctrica. Veamos un ejemplo:
1 neutróno [3] = 1 protón+ [2] + 1 electrón- [1]
1 neutróno [3] = 1 neutrinoo [1] + 1 positrón+ [1] + 1 electrón- [1]

La masa de las ruedas
Aprovechando la medición reciente del coeficiente de masas entre: el antiprotón (en realidad, el «oppo protón», porque se trata de materia común) y el protón, de la que ya he hablado al especular sobre el origen de la carga eléctrica, cuyo valor es R = 1,001089218755(64)(26); habiendo deducido, en el análisis del anexo II-6 de este documento, el número de quarks u y d que componen una rueda; y sabiendo la masa media de estos quarks, cuya mejor aproximación está en 3,42 ±0,09 MeV/c². Ahora podemos calcular la masa en reposo de las tres ruedas básicas que sirven para formar el resto de las entidades que acabamos de clasificar y que hemos aprendido a descomponer. Veámoslo:
Partimos del neutrino, una rueda neutra que no ha sufrido la transferencia de carga eléctrica, por tanto su masa en reposo se calcula sumando las masas de sus quarks.
Neutrino (νe) = 144 quarks u y d
Masa νe = 144 · 3,42±0,09 MeV/c² = 492,48±12,96 MeV/c² (entre 479,52 y 505,44 MeV/c²)
Ahora, planteamos un sistema de dos ecuaciones con dos incógnitas, usando: la descomposición del oppo protón, la del protón y su coeficiente de masas; Así como, el postulado elemental expuesto aquí, según el cual: la masa de una rueda neutra sería equivalente a la semisuma de las masas de una rueda con carga negativa y otra con carga positiva.
Electrón (e-) y Positrón (e+)
(νe + e-) / (νe + e+) = 1,001089218755
νe = (e- + e+) / 2
Resolviendo el sistema de ecuaciones obtenemos:
Masa e- = 493,01613±12,97411 MeV/c² (entre 480,04202 y 505,99024 MeV/c²)
Masa e+ = 491,94387±12,94589 MeV/c² (entre 478,99798 y 504,88976 MeV/c²)
Como vemos, la diferencia de masas en reposo de una rueda neutra y una con carga positiva o negativa es apenas de ± 0,535 MeV/c², con un margen de error 50 veces mayor. Lo que invita a usar, para ser prácticos, el valor de la masa en reposo de la rueda neutra en todas las ocasiones o, al menos, hasta que existan mediciones más precisas. Aún así practicaremos con un caso concreto:
A los taus electrónicos, se les ha medido una masa que es casi el doble de la del protón, lo que es una prueba empírica de que está formado por cuatro ruedas, pues son el resultado de la unión lineal de dos muones, uno con carga eléctrica y otro neutro. Hagamos su descomposición y la del protón, para averiguar el número de ruedas que los componen y la suma de las masas de estas:
1 tau electrón- [4] = 1 muón neutrinoº [2] + 1 muón electrón- [2]
1 muón neutrinoº [2] = 1 neutrinoº [1] + 1 neutrinoº [1]
1 muón electrón- [2] = 1 neutrinoº [1] + 1 electrón- [1]
1 tau electrón- [4] = 3 neutrinosº [3] + 1 electrón- [1]
Masa Т- = 3 · (492,48±12,96) + (493,01613±12,97411) = 1970,4561±12,9635 MeV/c²
1 protón+ [2] = 1 neutrinoº [1] + 1 positrón+ [1]
Masa p+ = (492,48±12,96) + (491,94387±12,94589) = 984,4239±12,9529 MeV/c²
El Tau electrónico es el resultado de la disposición lineal de tres neutrinos y un electrón. Esta unión es ineficaz para ir en una dirección concreta; pues se ve afectada por fuerzas electromagnéticas aplicadas fuera de su centro de masas, lo que provoca continuos cambios en su trayectoria y eso hace que su velocidad sea mucho menor. Esta reducción de su momento lineal es lo que hace que su masa relativista aparente se acerque a la suma de masas de sus ruedas y al doble de la del protón. Pero si queremos saber a qué velocidad aproximada debió moverse el tau electrónico, en el momento de la medición experimental de su masa, debemos aplicar las transformaciones de Lorentz. Considerando que las ruedas son giroscopios que tiene un momento angular, que somete a sus quarks a velocidades angulares relativistas, por tanto no sería correcto utilizar la masa en reposo de sus ruedas para calcular la cantidad de movimiento del tau. Para eso es mejor partir de la masa medida del protón, cuyas ruedas, en disposición opuesta, giran sin aplicar momento lineal alguno a este, es decir, consideraremos la masa de los taus, partiendo del número de ruedas que lo componen, sin pararnos a pensar en su carga eléctrica, y la multiplicaremos por la mitad del valor obtenido experimentalmente de la masa del protón, esto es, por la semimasa inercial aparente del protón (469.136 MeV/c²), que multiplicado por 4 nos da la masa inercial aparente del tau (1876,544 MeV/c²) considerando la velocidad angular de sus ruedas, pero sin considerar momento lineal alguno. Por tanto, como la masa del tau electrónico medida experimentalmente es 1776,99 MeV/c², la velocidad en el momento de la medida debió ser 0,321386 c (casi un tercio de la velocidad de la luz).